|
TOPICS
|
 |
 |
 |
|
Why Should You Use Nonlinear Curve Fitting?
Nonlinear curve fitting is by
far the most accurate way to reduce noise and
quantify peaks. Many instruments come with
software that only approximates the fitting
process by simply integrating the raw data
numerically. When there are shouldered or hidden
peaks, a lot of noise or a significant background
signal, this can lead to the wrong results. (For
example, a spectroscopy data set may appear to
have a peak with a 'raw' amplitude of 4,000 units
-- but may have a shoulder peak that distorts the
amplitude by 1,500 units! This would be a
significant error.)
PeakFit helps you separate overlapping peaks by
statistically fitting numerous peak functions to
one data set, which can help you find even the
most obscure patterns in your data. The background
can be fit as a separate polynomial, exponential,
logarithmic, hyperbolic or power model. This
fitted baseline is then subtracted before peak
characterization data (such as areas) is
calculated, which gives much more accurate
results. And any noise (like you get with
electrophoretic gels or Raman spectra) that might
bias raw data calculations is filtered simply by
the nonlinear curve fitting process. Nonlinear
curve fitting is essential for accurate peak
analysis and accurate research.
PeakFit Offers Sophisticated Data Manipulation
Back
To Top |
|
With PeakFit's visual FFT
filter, you can inspect your data stream in the
Fourier domain and zero higher frequency points --
and see your results immediately in the
time-domain. This smoothing technique allows for
superb noise reduction while maintaining the
integrity of the original data stream. PeakFit
also includes an automated FFT method as well as
Gaussian convolution, the Savitzky-Golay method
and the Loess algorithm for smoothing. AI Experts
throughout the smoothing options and other parts
of the program automatically help you to set many
adjustments. And, PeakFit even has a digital data
enhancer, which helps to analyze your sparse data.
Only PeakFit offers so many different methods of
data manipulation. |
|
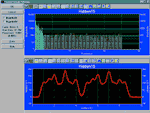
Click to View Larger Image |
| |
Highly Advanced Baseline Subtraction
|
|
PeakFit's
non-parametric baseline fitting routine easily
removes the complex background of a DNA
electrophoresis sample. PeakFit can also subtract
eight other built-in baseline equations or it can
subtract any baseline you've developed and stored
in a file. |
|

Click to View Larger Image |
| |
|
Full Graphical Placement of Peaks |
| |
|
If PeakFit's
auto-placement features fail on extremely
complicated or noisy data, you can place and fit
peaks graphically with only a few mouse clicks.
Each placed function has "anchors" that adjust
even the most highly complex functions,
automatically changing that function's specific
numeric parameters. PeakFit's graphical placement
options handle even the most complex peaks as
smoothly as Gaussians. |
| |
|
Publication-Quality Graphs and Data
Output |
| |
|
Every
publication-quality graph (see above) was created
using PeakFit's built-in graphic engine -- which
now includes print preview and extensive file and
clipboard export options. The numerical output is
customizable so that you see only the content you
want. |
| |
|
PeakFit Saves You Precious Research
Time |
| |
|
For most data sets,
PeakFit does all the work for you. What once took
hours now takes minutes – with only a few clicks
of the mouse! It’s so easy that novices can learn
how to use PeakFit in no time. And if you have
extremely complex or noisy data sets, the
sophistication and depth of PeakFit’s data
manipulation techniques is unequaled. |
| |
|
PeakFit Automatically Places Peaks in
Three Ways |
| |
|
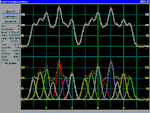
PeakFit uses three
procedures to automatically place hidden peaks;
while each is a strong solution, one method may
work better with some data sets than the others.
-
The
Residuals procedure initially places
peaks by finding local maxima in a smoothed data
stream. Hidden peaks are then optionally added
where peaks in the residuals occur.
-
The
Second Derivative procedure searches for
local minima within a smoothed second derivative
data stream. These local minima often reveal
hidden peaks.
-
The
Deconvolution procedure uses a Gaussian
response function with a Fourier deconvolution/
filtering algorithm. A successfully deconvolved
spec-trum will consist of “sharpened” peaks of
equivalent area. The goal is to enhance the
hidden peaks so that each represents a local
maximum.
|
|
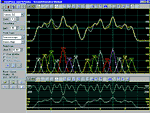
Click to View Larger Image
Click to View Larger Image |
| |